Unified (formula-based) interface version of the single-hidden-layer neural
network algorithm, possibly with skip-layer connections provided by
nnet::nnet().
mlNnet(train, ...)
ml_nnet(train, ...)
# S3 method for class 'formula'
mlNnet(
formula,
data,
size = NULL,
rang = NULL,
decay = 0,
maxit = 1000,
...,
subset,
na.action
)
# Default S3 method
mlNnet(train, response, size = NULL, rang = NULL, decay = 0, maxit = 1000, ...)
# S3 method for class 'mlNnet'
predict(
object,
newdata,
type = c("class", "membership", "both", "raw"),
method = c("direct", "cv"),
na.action = na.exclude,
...
)Arguments
- train
a matrix or data frame with predictors.
- ...
further arguments passed to
nnet::nnet()that has many more parameters (see its help page).- formula
a formula with left term being the factor variable to predict (for supervised classification), a vector of numbers (for regression) and the right term with the list of independent, predictive variables, separated with a plus sign. If the data frame provided contains only the dependent and independent variables, one can use the
class ~ .short version (that one is strongly encouraged). Variables with minus sign are eliminated. Calculations on variables are possible according to usual formula convention (possibly protected by usingI()).- data
a data.frame to use as a training set.
- size
number of units in the hidden layer. Can be zero if there are skip-layer units. If
NULL(the default), a reasonable value is computed.- rang
initial random weights on [-rang, rang]. Value about 0.5 unless the inputs are large, in which case it should be chosen so that rang * max(|x|) is about 1. If
NULL, a reasonable default is computed.- decay
parameter for weight decay. Default to 0.
- maxit
maximum number of iterations. Default 1000 (it is 100 in
nnet::nnet()).- subset
index vector with the cases to define the training set in use (this argument must be named, if provided).
- na.action
function to specify the action to be taken if
NAs are found. Forml_nnet()na.failis used by default. The calculation is stopped if there is anyNAin the data. Another option isna.omit, where cases with missing values on any required variable are dropped (this argument must be named, if provided). For thepredict()method, the default, and most suitable option, isna.exclude. In that case, rows withNAs innewdata=are excluded from prediction, but reinjected in the final results so that the number of items is still the same (and in the same order asnewdata=).- response
a vector of factor (classification) or numeric (regression).
- object
an mlNnet object
- newdata
a new dataset with same conformation as the training set (same variables, except may by the class for classification or dependent variable for regression). Usually a test set, or a new dataset to be predicted.
- type
the type of prediction to return.
"class"by default, the predicted classes. Other options are"membership"the membership (number between 0 and 1) to the different classes, or"both"to return classes and memberships. Also type"raw"as non normalized result as returned bynnet::nnet()(useful for regression, see examples).- method
"direct"(default) or"cv"."direct"predicts new cases innewdata=if this argument is provided, or the cases in the training set if not. Take care that not providingnewdata=means that you just calculate the self-consistency of the classifier but cannot use the metrics derived from these results for the assessment of its performances. Either use a different data set innewdata=or use the alternate cross-validation ("cv") technique. If you specifymethod = "cv"thencvpredict()is used and you cannot providenewdata=in that case.
Value
ml_nnet()/mlNnet() creates an mlNnet, mlearning object
containing the classifier and a lot of additional metadata used by the
functions and methods you can apply to it like predict() or
cvpredict(). In case you want to program new functions or extract
specific components, inspect the "unclassed" object using unclass().
See also
mlearning(), cvpredict(), confusion(), also nnet::nnet()
that actually does the classification.
Examples
# Prepare data: split into training set (2/3) and test set (1/3)
data("iris", package = "datasets")
train <- c(1:34, 51:83, 101:133)
iris_train <- iris[train, ]
iris_test <- iris[-train, ]
# One case with missing data in train set, and another case in test set
iris_train[1, 1] <- NA
iris_test[25, 2] <- NA
set.seed(689) # Useful for reproductibility, use a different value each time!
iris_nnet <- ml_nnet(data = iris_train, Species ~ .)
#> # weights: 19
#> initial value 109.026448
#> iter 10 value 39.094573
#> iter 20 value 5.901073
#> iter 30 value 0.126987
#> iter 40 value 0.000192
#> final value 0.000054
#> converged
summary(iris_nnet)
#> A mlearning object of class mlNnet (single-hidden-layer neural network):
#> Initial call: mlNnet.formula(formula = Species ~ ., data = iris_train)
#> a 4-2-3 network with 19 weights
#> options were - softmax modelling
#> b->h1 i1->h1 i2->h1 i3->h1 i4->h1
#> -42.30 -213.56 -147.78 -62.49 -10.54
#> b->h2 i1->h2 i2->h2 i3->h2 i4->h2
#> -3.14 -0.13 -1.10 0.78 2.82
#> b->o1 h1->o1 h2->o1
#> 188.59 46.07 -343.82
#> b->o2 h1->o2 h2->o2
#> 146.83 -16.17 -121.13
#> b->o3 h1->o3 h2->o3
#> -335.40 -29.85 464.76
predict(iris_nnet) # Default type is class
#> [1] setosa setosa setosa setosa setosa setosa
#> [7] setosa setosa setosa setosa setosa setosa
#> [13] setosa setosa setosa setosa setosa setosa
#> [19] setosa setosa setosa setosa setosa setosa
#> [25] setosa setosa setosa setosa setosa setosa
#> [31] setosa setosa setosa versicolor versicolor versicolor
#> [37] versicolor versicolor versicolor versicolor versicolor versicolor
#> [43] versicolor versicolor versicolor versicolor versicolor versicolor
#> [49] versicolor versicolor versicolor versicolor versicolor versicolor
#> [55] versicolor versicolor versicolor versicolor versicolor versicolor
#> [61] versicolor versicolor versicolor versicolor versicolor versicolor
#> [67] virginica virginica virginica virginica virginica virginica
#> [73] virginica virginica virginica virginica virginica virginica
#> [79] virginica virginica virginica virginica virginica virginica
#> [85] virginica virginica virginica virginica virginica virginica
#> [91] virginica virginica virginica virginica virginica virginica
#> [97] virginica virginica virginica
#> Levels: setosa versicolor virginica
predict(iris_nnet, type = "membership")
#> setosa versicolor virginica
#> [1,] 1.000000e+00 1.981261e-18 9.954308e-227
#> [2,] 1.000000e+00 1.563429e-18 4.212192e-227
#> [3,] 1.000000e+00 1.991958e-18 1.015086e-226
#> [4,] 1.000000e+00 1.218574e-18 1.704251e-227
#> [5,] 1.000000e+00 1.581490e-18 4.391585e-227
#> [6,] 1.000000e+00 1.768573e-18 6.590714e-227
#> [7,] 1.000000e+00 1.452927e-18 3.227868e-227
#> [8,] 1.000000e+00 2.388205e-18 1.961545e-226
#> [9,] 1.000000e+00 1.517479e-18 3.779780e-227
#> [10,] 1.000000e+00 1.170688e-18 1.473378e-227
#> [11,] 1.000000e+00 1.564473e-18 4.222421e-227
#> [12,] 1.000000e+00 1.568725e-18 4.264236e-227
#> [13,] 1.000000e+00 1.392460e-18 2.766197e-227
#> [14,] 1.000000e+00 9.449426e-19 6.768557e-228
#> [15,] 1.000000e+00 1.057297e-18 1.017797e-227
#> [16,] 1.000000e+00 1.287978e-18 2.083934e-227
#> [17,] 1.000000e+00 1.538456e-18 3.972978e-227
#> [18,] 1.000000e+00 1.368858e-18 2.599712e-227
#> [19,] 1.000000e+00 1.304507e-18 2.182693e-227
#> [20,] 1.000000e+00 1.567544e-18 4.252587e-227
#> [21,] 1.000000e+00 1.717278e-18 5.922687e-227
#> [22,] 1.000000e+00 1.084511e-18 1.116184e-227
#> [23,] 1.000000e+00 5.626048e-18 4.403810e-225
#> [24,] 1.000000e+00 1.908550e-18 8.690599e-227
#> [25,] 1.000000e+00 2.307574e-18 1.731561e-226
#> [26,] 1.000000e+00 2.675016e-18 2.961044e-226
#> [27,] 1.000000e+00 1.332828e-18 2.359724e-227
#> [28,] 1.000000e+00 1.359101e-18 2.533053e-227
#> [29,] 1.000000e+00 1.906942e-18 8.664044e-227
#> [30,] 1.000000e+00 2.102434e-18 1.234872e-226
#> [31,] 1.000000e+00 2.290961e-18 1.686721e-226
#> [32,] 1.000000e+00 9.262816e-19 6.295678e-228
#> [33,] 1.000000e+00 9.386502e-19 6.606327e-228
#> [34,] 1.696393e-32 1.000000e+00 7.388244e-79
#> [35,] 2.536259e-37 1.000000e+00 3.666456e-66
#> [36,] 1.385692e-45 1.000000e+00 2.010898e-44
#> [37,] 6.596643e-41 1.000000e+00 9.913570e-57
#> [38,] 9.642900e-49 1.000000e+00 4.081612e-36
#> [39,] 1.633207e-36 1.000000e+00 2.729769e-68
#> [40,] 3.755319e-45 1.000000e+00 1.459475e-45
#> [41,] 1.959318e-08 1.000000e+00 3.619331e-142
#> [42,] 5.103285e-33 1.000000e+00 1.742208e-77
#> [43,] 3.411322e-36 1.000000e+00 3.930977e-69
#> [44,] 7.470698e-21 1.000000e+00 1.710007e-109
#> [45,] 1.713477e-38 1.000000e+00 4.399548e-63
#> [46,] 7.171178e-22 1.000000e+00 8.143408e-107
#> [47,] 5.543993e-43 1.000000e+00 2.864052e-51
#> [48,] 1.519393e-17 1.000000e+00 3.378024e-118
#> [49,] 2.045539e-30 1.000000e+00 2.469336e-84
#> [50,] 9.761421e-45 1.000000e+00 1.182121e-46
#> [51,] 5.488221e-12 1.000000e+00 8.051914e-133
#> [52,] 4.410224e-60 9.999972e-01 2.794471e-06
#> [53,] 4.371794e-20 1.000000e+00 1.637552e-111
#> [54,] 2.738495e-60 9.999902e-01 9.789977e-06
#> [55,] 6.677921e-26 1.000000e+00 3.284325e-96
#> [56,] 1.358014e-59 9.999999e-01 1.449382e-07
#> [57,] 2.769750e-32 1.000000e+00 2.034009e-79
#> [58,] 5.720934e-28 1.000000e+00 9.021752e-91
#> [59,] 2.188126e-33 1.000000e+00 1.617118e-76
#> [60,] 3.139089e-45 1.000000e+00 2.338872e-45
#> [61,] 3.324344e-60 9.999941e-01 5.878531e-06
#> [62,] 4.647318e-46 1.000000e+00 3.562305e-43
#> [63,] 1.989700e-05 9.999801e-01 4.444841e-150
#> [64,] 4.028926e-21 1.000000e+00 8.681052e-109
#> [65,] 3.708411e-13 1.000000e+00 9.657659e-130
#> [66,] 6.520096e-21 1.000000e+00 2.446313e-109
#> [67,] 6.639578e-119 8.071938e-42 1.000000e+00
#> [68,] 2.180618e-97 3.145877e-26 1.000000e+00
#> [69,] 2.539473e-110 1.336328e-35 1.000000e+00
#> [70,] 1.064604e-92 7.854112e-23 1.000000e+00
#> [71,] 1.254516e-113 5.372777e-38 1.000000e+00
#> [72,] 1.481366e-115 2.154316e-39 1.000000e+00
#> [73,] 4.403234e-74 2.424556e-09 1.000000e+00
#> [74,] 6.760041e-103 3.207750e-30 1.000000e+00
#> [75,] 2.629593e-105 5.752754e-32 1.000000e+00
#> [76,] 1.463118e-116 4.025418e-40 1.000000e+00
#> [77,] 5.092016e-87 1.024699e-18 1.000000e+00
#> [78,] 2.510455e-99 1.238431e-27 1.000000e+00
#> [79,] 3.968675e-106 1.461521e-32 1.000000e+00
#> [80,] 1.943255e-106 8.711557e-33 1.000000e+00
#> [81,] 1.552111e-116 4.201383e-40 1.000000e+00
#> [82,] 8.298563e-110 3.151694e-35 1.000000e+00
#> [83,] 5.440640e-86 5.702084e-18 1.000000e+00
#> [84,] 1.326191e-109 4.426643e-35 1.000000e+00
#> [85,] 1.052184e-121 7.552117e-44 1.000000e+00
#> [86,] 6.402383e-75 5.995593e-10 1.000000e+00
#> [87,] 6.599996e-113 1.789299e-37 1.000000e+00
#> [88,] 2.243228e-98 6.054134e-27 1.000000e+00
#> [89,] 1.356615e-115 2.021275e-39 1.000000e+00
#> [90,] 5.449674e-82 4.518006e-15 1.000000e+00
#> [91,] 4.102581e-103 2.233783e-30 1.000000e+00
#> [92,] 1.092023e-88 6.331265e-20 1.000000e+00
#> [93,] 5.403221e-75 5.301971e-10 1.000000e+00
#> [94,] 3.242733e-69 8.153604e-06 9.999918e-01
#> [95,] 2.728115e-111 2.653774e-36 1.000000e+00
#> [96,] 2.992629e-69 7.692923e-06 9.999923e-01
#> [97,] 5.651859e-107 3.560132e-33 1.000000e+00
#> [98,] 1.643945e-92 1.076039e-22 1.000000e+00
#> [99,] 2.121284e-114 1.482171e-38 1.000000e+00
predict(iris_nnet, type = "both")
#> $class
#> [1] setosa setosa setosa setosa setosa setosa
#> [7] setosa setosa setosa setosa setosa setosa
#> [13] setosa setosa setosa setosa setosa setosa
#> [19] setosa setosa setosa setosa setosa setosa
#> [25] setosa setosa setosa setosa setosa setosa
#> [31] setosa setosa setosa versicolor versicolor versicolor
#> [37] versicolor versicolor versicolor versicolor versicolor versicolor
#> [43] versicolor versicolor versicolor versicolor versicolor versicolor
#> [49] versicolor versicolor versicolor versicolor versicolor versicolor
#> [55] versicolor versicolor versicolor versicolor versicolor versicolor
#> [61] versicolor versicolor versicolor versicolor versicolor versicolor
#> [67] virginica virginica virginica virginica virginica virginica
#> [73] virginica virginica virginica virginica virginica virginica
#> [79] virginica virginica virginica virginica virginica virginica
#> [85] virginica virginica virginica virginica virginica virginica
#> [91] virginica virginica virginica virginica virginica virginica
#> [97] virginica virginica virginica
#> Levels: setosa versicolor virginica
#>
#> $membership
#> setosa versicolor virginica
#> [1,] 1.000000e+00 1.981261e-18 9.954308e-227
#> [2,] 1.000000e+00 1.563429e-18 4.212192e-227
#> [3,] 1.000000e+00 1.991958e-18 1.015086e-226
#> [4,] 1.000000e+00 1.218574e-18 1.704251e-227
#> [5,] 1.000000e+00 1.581490e-18 4.391585e-227
#> [6,] 1.000000e+00 1.768573e-18 6.590714e-227
#> [7,] 1.000000e+00 1.452927e-18 3.227868e-227
#> [8,] 1.000000e+00 2.388205e-18 1.961545e-226
#> [9,] 1.000000e+00 1.517479e-18 3.779780e-227
#> [10,] 1.000000e+00 1.170688e-18 1.473378e-227
#> [11,] 1.000000e+00 1.564473e-18 4.222421e-227
#> [12,] 1.000000e+00 1.568725e-18 4.264236e-227
#> [13,] 1.000000e+00 1.392460e-18 2.766197e-227
#> [14,] 1.000000e+00 9.449426e-19 6.768557e-228
#> [15,] 1.000000e+00 1.057297e-18 1.017797e-227
#> [16,] 1.000000e+00 1.287978e-18 2.083934e-227
#> [17,] 1.000000e+00 1.538456e-18 3.972978e-227
#> [18,] 1.000000e+00 1.368858e-18 2.599712e-227
#> [19,] 1.000000e+00 1.304507e-18 2.182693e-227
#> [20,] 1.000000e+00 1.567544e-18 4.252587e-227
#> [21,] 1.000000e+00 1.717278e-18 5.922687e-227
#> [22,] 1.000000e+00 1.084511e-18 1.116184e-227
#> [23,] 1.000000e+00 5.626048e-18 4.403810e-225
#> [24,] 1.000000e+00 1.908550e-18 8.690599e-227
#> [25,] 1.000000e+00 2.307574e-18 1.731561e-226
#> [26,] 1.000000e+00 2.675016e-18 2.961044e-226
#> [27,] 1.000000e+00 1.332828e-18 2.359724e-227
#> [28,] 1.000000e+00 1.359101e-18 2.533053e-227
#> [29,] 1.000000e+00 1.906942e-18 8.664044e-227
#> [30,] 1.000000e+00 2.102434e-18 1.234872e-226
#> [31,] 1.000000e+00 2.290961e-18 1.686721e-226
#> [32,] 1.000000e+00 9.262816e-19 6.295678e-228
#> [33,] 1.000000e+00 9.386502e-19 6.606327e-228
#> [34,] 1.696393e-32 1.000000e+00 7.388244e-79
#> [35,] 2.536259e-37 1.000000e+00 3.666456e-66
#> [36,] 1.385692e-45 1.000000e+00 2.010898e-44
#> [37,] 6.596643e-41 1.000000e+00 9.913570e-57
#> [38,] 9.642900e-49 1.000000e+00 4.081612e-36
#> [39,] 1.633207e-36 1.000000e+00 2.729769e-68
#> [40,] 3.755319e-45 1.000000e+00 1.459475e-45
#> [41,] 1.959318e-08 1.000000e+00 3.619331e-142
#> [42,] 5.103285e-33 1.000000e+00 1.742208e-77
#> [43,] 3.411322e-36 1.000000e+00 3.930977e-69
#> [44,] 7.470698e-21 1.000000e+00 1.710007e-109
#> [45,] 1.713477e-38 1.000000e+00 4.399548e-63
#> [46,] 7.171178e-22 1.000000e+00 8.143408e-107
#> [47,] 5.543993e-43 1.000000e+00 2.864052e-51
#> [48,] 1.519393e-17 1.000000e+00 3.378024e-118
#> [49,] 2.045539e-30 1.000000e+00 2.469336e-84
#> [50,] 9.761421e-45 1.000000e+00 1.182121e-46
#> [51,] 5.488221e-12 1.000000e+00 8.051914e-133
#> [52,] 4.410224e-60 9.999972e-01 2.794471e-06
#> [53,] 4.371794e-20 1.000000e+00 1.637552e-111
#> [54,] 2.738495e-60 9.999902e-01 9.789977e-06
#> [55,] 6.677921e-26 1.000000e+00 3.284325e-96
#> [56,] 1.358014e-59 9.999999e-01 1.449382e-07
#> [57,] 2.769750e-32 1.000000e+00 2.034009e-79
#> [58,] 5.720934e-28 1.000000e+00 9.021752e-91
#> [59,] 2.188126e-33 1.000000e+00 1.617118e-76
#> [60,] 3.139089e-45 1.000000e+00 2.338872e-45
#> [61,] 3.324344e-60 9.999941e-01 5.878531e-06
#> [62,] 4.647318e-46 1.000000e+00 3.562305e-43
#> [63,] 1.989700e-05 9.999801e-01 4.444841e-150
#> [64,] 4.028926e-21 1.000000e+00 8.681052e-109
#> [65,] 3.708411e-13 1.000000e+00 9.657659e-130
#> [66,] 6.520096e-21 1.000000e+00 2.446313e-109
#> [67,] 6.639578e-119 8.071938e-42 1.000000e+00
#> [68,] 2.180618e-97 3.145877e-26 1.000000e+00
#> [69,] 2.539473e-110 1.336328e-35 1.000000e+00
#> [70,] 1.064604e-92 7.854112e-23 1.000000e+00
#> [71,] 1.254516e-113 5.372777e-38 1.000000e+00
#> [72,] 1.481366e-115 2.154316e-39 1.000000e+00
#> [73,] 4.403234e-74 2.424556e-09 1.000000e+00
#> [74,] 6.760041e-103 3.207750e-30 1.000000e+00
#> [75,] 2.629593e-105 5.752754e-32 1.000000e+00
#> [76,] 1.463118e-116 4.025418e-40 1.000000e+00
#> [77,] 5.092016e-87 1.024699e-18 1.000000e+00
#> [78,] 2.510455e-99 1.238431e-27 1.000000e+00
#> [79,] 3.968675e-106 1.461521e-32 1.000000e+00
#> [80,] 1.943255e-106 8.711557e-33 1.000000e+00
#> [81,] 1.552111e-116 4.201383e-40 1.000000e+00
#> [82,] 8.298563e-110 3.151694e-35 1.000000e+00
#> [83,] 5.440640e-86 5.702084e-18 1.000000e+00
#> [84,] 1.326191e-109 4.426643e-35 1.000000e+00
#> [85,] 1.052184e-121 7.552117e-44 1.000000e+00
#> [86,] 6.402383e-75 5.995593e-10 1.000000e+00
#> [87,] 6.599996e-113 1.789299e-37 1.000000e+00
#> [88,] 2.243228e-98 6.054134e-27 1.000000e+00
#> [89,] 1.356615e-115 2.021275e-39 1.000000e+00
#> [90,] 5.449674e-82 4.518006e-15 1.000000e+00
#> [91,] 4.102581e-103 2.233783e-30 1.000000e+00
#> [92,] 1.092023e-88 6.331265e-20 1.000000e+00
#> [93,] 5.403221e-75 5.301971e-10 1.000000e+00
#> [94,] 3.242733e-69 8.153604e-06 9.999918e-01
#> [95,] 2.728115e-111 2.653774e-36 1.000000e+00
#> [96,] 2.992629e-69 7.692923e-06 9.999923e-01
#> [97,] 5.651859e-107 3.560132e-33 1.000000e+00
#> [98,] 1.643945e-92 1.076039e-22 1.000000e+00
#> [99,] 2.121284e-114 1.482171e-38 1.000000e+00
#>
# Self-consistency, do not use for assessing classifier performances!
confusion(iris_nnet)
#> 99 items classified with 99 true positives (error rate = 0%)
#> Predicted
#> Actual 01 02 03 (sum) (FNR%)
#> 01 virginica 33 0 0 33 0
#> 02 setosa 0 33 0 33 0
#> 03 versicolor 0 0 33 33 0
#> (sum) 33 33 33 99 0
# Use an independent test set instead
confusion(predict(iris_nnet, newdata = iris_test), iris_test$Species)
#> 50 items classified with 47 true positives (error rate = 6%)
#> Predicted
#> Actual 01 02 03 04 (sum) (FNR%)
#> 01 setosa 16 0 0 0 16 0
#> 02 NA 0 0 0 0 0
#> 03 versicolor 0 1 15 1 17 12
#> 04 virginica 0 0 1 16 17 6
#> (sum) 16 1 16 17 50 6
# Idem, but two classes prediction
data("HouseVotes84", package = "mlbench")
set.seed(325)
house_nnet <- ml_nnet(data = HouseVotes84, Class ~ ., na.action = na.omit)
#> # weights: 19
#> initial value 169.309559
#> iter 10 value 56.372600
#> iter 20 value 25.973675
#> iter 30 value 13.853049
#> iter 40 value 13.799839
#> iter 50 value 13.777997
#> iter 60 value 11.056490
#> iter 70 value 10.065342
#> iter 80 value 10.031942
#> iter 90 value 10.015482
#> iter 100 value 10.013087
#> iter 110 value 10.011137
#> iter 120 value 10.008720
#> iter 130 value 10.005719
#> iter 140 value 10.004402
#> iter 150 value 10.003256
#> iter 160 value 10.002171
#> iter 170 value 10.001886
#> iter 180 value 10.001430
#> iter 190 value 10.001084
#> iter 200 value 10.000223
#> iter 210 value 9.999774
#> iter 220 value 9.999346
#> iter 230 value 9.998816
#> iter 240 value 9.998468
#> iter 250 value 9.998363
#> iter 260 value 9.998319
#> iter 270 value 9.998238
#> iter 280 value 9.998194
#> iter 290 value 9.997054
#> iter 300 value 9.996987
#> iter 310 value 9.996838
#> iter 320 value 9.996751
#> final value 9.996749
#> converged
summary(house_nnet)
#> A mlearning object of class mlNnet (single-hidden-layer neural network):
#> Initial call: mlNnet.formula(formula = Class ~ ., data = HouseVotes84, na.action = na.omit)
#> a 16-1-1 network with 19 weights
#> options were - entropy fitting
#> b->h1 i1->h1 i2->h1 i3->h1 i4->h1 i5->h1 i6->h1 i7->h1 i8->h1 i9->h1
#> -25.97 8.30 8.57 -26.71 52.83 0.18 -7.20 12.39 -12.27 -11.17
#> i10->h1 i11->h1 i12->h1 i13->h1 i14->h1 i15->h1 i16->h1
#> 14.87 -30.35 5.41 -11.96 5.94 -7.00 9.42
#> b->o h1->o
#> -26.46 30.45
# Cross-validated confusion matrix
confusion(cvpredict(house_nnet), na.omit(HouseVotes84)$Class)
#> # weights: 19
#> initial value 143.717759
#> iter 10 value 18.848757
#> iter 20 value 9.444928
#> iter 30 value 6.417139
#> iter 40 value 5.774767
#> iter 50 value 5.621749
#> iter 60 value 5.585126
#> iter 70 value 5.583271
#> iter 80 value 5.582734
#> iter 90 value 5.581081
#> iter 100 value 5.580656
#> iter 110 value 5.580538
#> iter 120 value 5.580411
#> iter 130 value 5.580388
#> iter 140 value 5.580370
#> iter 150 value 5.580355
#> iter 160 value 5.580332
#> iter 170 value 5.580127
#> final value 5.580121
#> converged
#> # weights: 19
#> initial value 143.812486
#> iter 10 value 30.720972
#> iter 20 value 9.782350
#> iter 30 value 5.604171
#> iter 40 value 5.514307
#> iter 50 value 0.093468
#> iter 60 value 0.016101
#> iter 70 value 0.005208
#> iter 80 value 0.002482
#> iter 90 value 0.001895
#> iter 100 value 0.001498
#> iter 110 value 0.001053
#> iter 120 value 0.000671
#> iter 130 value 0.000593
#> iter 140 value 0.000474
#> iter 150 value 0.000410
#> iter 160 value 0.000309
#> iter 170 value 0.000223
#> iter 180 value 0.000210
#> iter 190 value 0.000132
#> iter 200 value 0.000106
#> final value 0.000099
#> converged
#> # weights: 19
#> initial value 145.016337
#> iter 10 value 10.046476
#> iter 20 value 0.116477
#> iter 30 value 0.000132
#> iter 30 value 0.000063
#> iter 30 value 0.000059
#> final value 0.000059
#> converged
#> # weights: 19
#> initial value 144.235058
#> iter 10 value 15.299952
#> iter 20 value 13.546904
#> iter 30 value 13.466835
#> iter 40 value 11.189888
#> iter 50 value 9.894254
#> iter 60 value 9.831545
#> iter 70 value 9.808962
#> iter 80 value 9.795122
#> iter 90 value 9.793556
#> iter 100 value 9.791575
#> iter 110 value 9.791049
#> iter 120 value 9.790586
#> iter 130 value 9.790261
#> iter 140 value 9.789627
#> iter 150 value 9.789211
#> iter 160 value 9.788917
#> iter 170 value 9.788296
#> iter 180 value 9.787547
#> iter 190 value 9.787253
#> iter 200 value 9.787207
#> iter 210 value 9.787004
#> iter 220 value 9.786783
#> iter 230 value 9.785834
#> iter 240 value 9.785472
#> iter 250 value 9.784911
#> iter 260 value 9.784756
#> iter 270 value 9.784424
#> final value 9.784419
#> converged
#> # weights: 19
#> initial value 145.290442
#> iter 10 value 23.029519
#> iter 20 value 13.559441
#> iter 30 value 12.126742
#> iter 40 value 5.965420
#> iter 50 value 1.326633
#> iter 60 value 0.098605
#> iter 70 value 0.014886
#> iter 80 value 0.004322
#> iter 90 value 0.002398
#> iter 100 value 0.001729
#> iter 110 value 0.000896
#> iter 120 value 0.000614
#> iter 130 value 0.000434
#> iter 140 value 0.000375
#> iter 150 value 0.000311
#> iter 160 value 0.000218
#> iter 170 value 0.000191
#> iter 180 value 0.000186
#> iter 190 value 0.000162
#> iter 200 value 0.000134
#> iter 210 value 0.000124
#> iter 220 value 0.000122
#> iter 230 value 0.000109
#> final value 0.000098
#> converged
#> # weights: 19
#> initial value 136.866761
#> iter 10 value 10.055239
#> iter 20 value 9.042402
#> iter 30 value 0.462250
#> iter 40 value 0.013432
#> iter 50 value 0.002624
#> iter 60 value 0.000764
#> iter 70 value 0.000586
#> iter 80 value 0.000152
#> iter 90 value 0.000143
#> iter 100 value 0.000143
#> iter 110 value 0.000140
#> iter 120 value 0.000140
#> iter 120 value 0.000140
#> final value 0.000140
#> converged
#> # weights: 19
#> initial value 145.921787
#> iter 10 value 51.158020
#> iter 20 value 20.204569
#> iter 30 value 19.954583
#> iter 40 value 19.953281
#> iter 50 value 19.953130
#> iter 50 value 19.953130
#> iter 50 value 19.953130
#> final value 19.953130
#> converged
#> # weights: 19
#> initial value 146.064948
#> iter 10 value 18.762028
#> iter 20 value 5.130610
#> iter 30 value 0.027649
#> final value 0.000051
#> converged
#> # weights: 19
#> initial value 153.194181
#> iter 10 value 37.154579
#> iter 20 value 5.531590
#> iter 30 value 2.236234
#> iter 40 value 0.176689
#> iter 50 value 0.010148
#> iter 60 value 0.000397
#> iter 70 value 0.000179
#> final value 0.000081
#> converged
#> # weights: 19
#> initial value 148.213782
#> iter 10 value 20.337335
#> iter 20 value 1.795220
#> iter 30 value 0.003358
#> final value 0.000057
#> converged
#> 232 items classified with 219 true positives (error rate = 5.6%)
#> Predicted
#> Actual 01 02 (sum) (FNR%)
#> 01 democrat 115 9 124 7
#> 02 republican 4 104 108 4
#> (sum) 119 113 232 6
# Regression
data(airquality, package = "datasets")
set.seed(74)
ozone_nnet <- ml_nnet(data = airquality, Ozone ~ ., na.action = na.omit,
skip = TRUE, decay = 1e-3, size = 20, linout = TRUE)
#> # weights: 146
#> initial value 329959.371356
#> iter 10 value 52446.220833
#> iter 20 value 49603.490076
#> iter 30 value 46259.519458
#> iter 40 value 44142.030523
#> iter 50 value 43250.816616
#> iter 60 value 39852.930471
#> iter 70 value 36766.639329
#> iter 80 value 36359.340847
#> iter 90 value 35067.999132
#> iter 100 value 34179.089643
#> iter 110 value 33104.742531
#> iter 120 value 32109.128326
#> iter 130 value 30504.969695
#> iter 140 value 29816.599569
#> iter 150 value 29768.593874
#> iter 160 value 29744.667394
#> iter 170 value 29669.107831
#> iter 180 value 29597.956072
#> iter 190 value 29560.077614
#> iter 200 value 29383.233180
#> iter 210 value 29327.895164
#> iter 220 value 29207.975099
#> iter 230 value 29123.797795
#> iter 240 value 29003.256685
#> iter 250 value 28921.883585
#> iter 260 value 28819.788764
#> iter 270 value 28707.201615
#> iter 280 value 28626.060649
#> iter 290 value 28612.478500
#> iter 300 value 28595.835225
#> iter 310 value 28524.664792
#> iter 320 value 28475.905238
#> iter 330 value 28348.265526
#> iter 340 value 28315.347852
#> iter 350 value 28314.082408
#> iter 350 value 28314.082371
#> iter 350 value 28314.082213
#> final value 28314.082213
#> converged
summary(ozone_nnet)
#> A mlearning object of class mlNnet (single-hidden-layer neural network):
#> [regression variant]
#> Initial call: mlNnet.formula(formula = Ozone ~ ., data = airquality, size = 20, decay = 0.001, skip = TRUE, linout = TRUE, na.action = na.omit)
#> a 5-20-1 network with 146 weights
#> options were - skip-layer connections linear output units decay=0.001
#> b->h1 i1->h1 i2->h1 i3->h1 i4->h1 i5->h1
#> -0.76 5.72 -16.12 -11.64 -5.74 -13.39
#> b->h2 i1->h2 i2->h2 i3->h2 i4->h2 i5->h2
#> -0.01 1.39 0.07 0.06 0.02 -0.10
#> b->h3 i1->h3 i2->h3 i3->h3 i4->h3 i5->h3
#> -0.29 0.85 -7.25 2.90 -8.27 -3.13
#> b->h4 i1->h4 i2->h4 i3->h4 i4->h4 i5->h4
#> 0.03 1.59 -0.19 3.13 0.24 0.78
#> b->h5 i1->h5 i2->h5 i3->h5 i4->h5 i5->h5
#> 7.94 2.46 -23.57 1.39 -4.07 -16.10
#> b->h6 i1->h6 i2->h6 i3->h6 i4->h6 i5->h6
#> 0.01 1.65 0.32 0.62 0.09 0.02
#> b->h7 i1->h7 i2->h7 i3->h7 i4->h7 i5->h7
#> 0.01 0.67 0.12 0.58 0.07 0.07
#> b->h8 i1->h8 i2->h8 i3->h8 i4->h8 i5->h8
#> 0.06 0.38 0.94 2.91 0.39 0.83
#> b->h9 i1->h9 i2->h9 i3->h9 i4->h9 i5->h9
#> 0.29 2.47 1.59 1.14 4.24 -6.88
#> b->h10 i1->h10 i2->h10 i3->h10 i4->h10 i5->h10
#> 0.01 3.49 0.10 0.00 0.01 -0.16
#> b->h11 i1->h11 i2->h11 i3->h11 i4->h11 i5->h11
#> 0.01 1.91 0.22 0.66 0.09 0.07
#> b->h12 i1->h12 i2->h12 i3->h12 i4->h12 i5->h12
#> 0.04 1.56 0.72 2.32 0.28 0.55
#> b->h13 i1->h13 i2->h13 i3->h13 i4->h13 i5->h13
#> -1.44 3.53 -4.33 -17.18 -6.21 20.59
#> b->h14 i1->h14 i2->h14 i3->h14 i4->h14 i5->h14
#> 0.07 7.32 1.08 3.59 0.45 1.02
#> b->h15 i1->h15 i2->h15 i3->h15 i4->h15 i5->h15
#> 0.16 -8.91 1.17 8.40 1.56 -0.64
#> b->h16 i1->h16 i2->h16 i3->h16 i4->h16 i5->h16
#> -2.17 3.02 -21.18 0.78 -6.75 -2.44
#> b->h17 i1->h17 i2->h17 i3->h17 i4->h17 i5->h17
#> 0.04 2.61 0.68 3.06 0.34 0.75
#> b->h18 i1->h18 i2->h18 i3->h18 i4->h18 i5->h18
#> -0.06 3.87 -1.93 -0.72 -0.72 -1.01
#> b->h19 i1->h19 i2->h19 i3->h19 i4->h19 i5->h19
#> -0.04 6.47 -0.99 -2.31 -0.55 -0.90
#> b->h20 i1->h20 i2->h20 i3->h20 i4->h20 i5->h20
#> 0.01 2.75 0.06 -0.02 0.00 -0.13
#> b->o h1->o h2->o h3->o h4->o h5->o h6->o h7->o h8->o h9->o h10->o
#> -9.17 -30.81 -1.46 -36.98 0.41 9.42 2.41 -1.54 3.12 26.63 3.55
#> h11->o h12->o h13->o h14->o h15->o h16->o h17->o h18->o h19->o h20->o i1->o
#> 0.20 5.03 -19.61 2.28 -16.38 -46.10 2.63 -15.19 1.10 5.83 0.32
#> i2->o i3->o i4->o i5->o
#> -4.68 1.29 -1.95 0.06
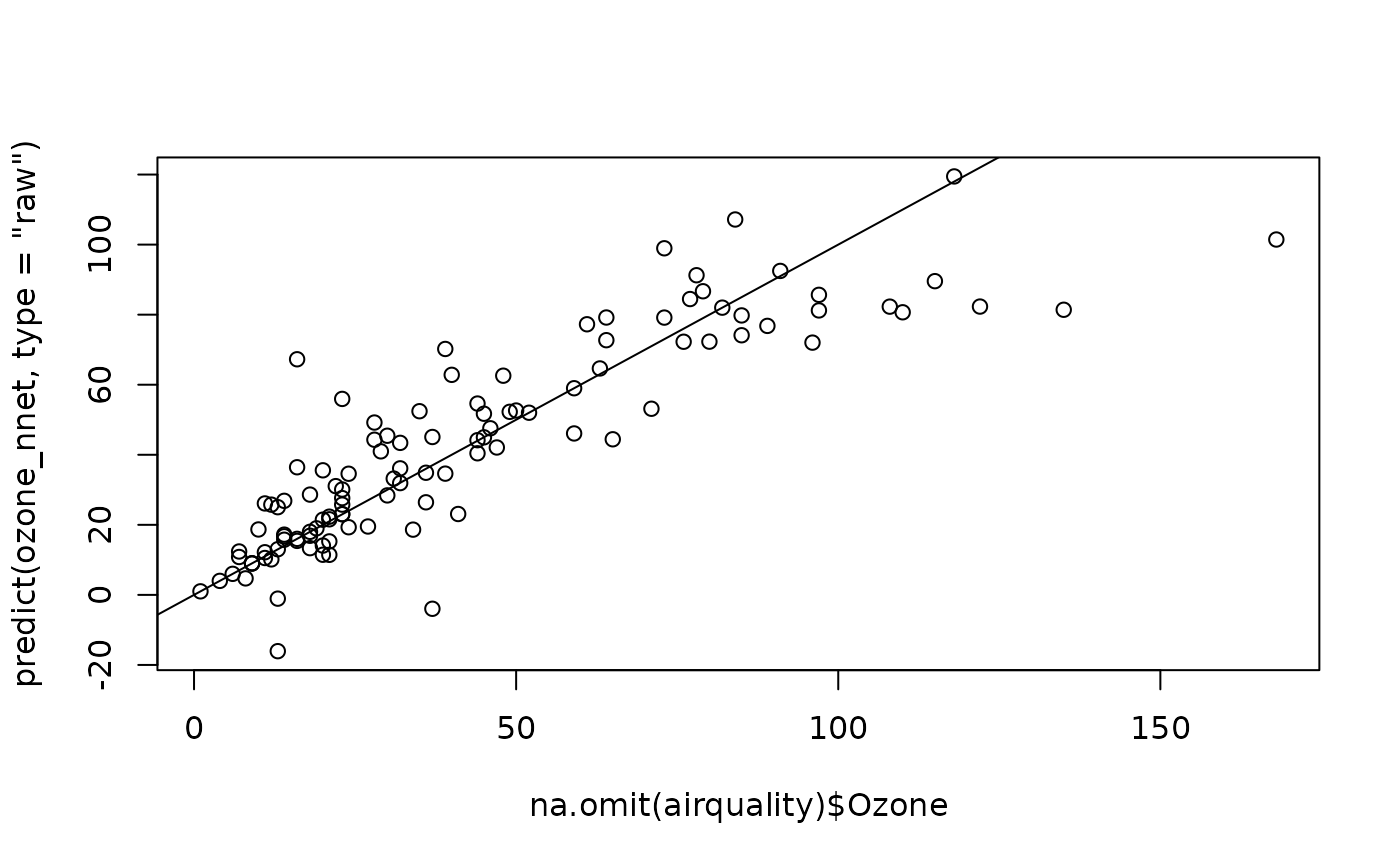
plot(na.omit(airquality)$Ozone, predict(ozone_nnet, type = "raw"))
abline(a = 0, b = 1)